Project: Comparison of E(n)-equivariant GNNs for metamaterial simulation
Description
Soft, porous metamaterials are materials that consist of a flexible base material (e.g., rubber-like material) with pores of a carefully designed shape in it. Under external loading (a pressure applied on the outside surface, mechanical constraints, or other interactions), they deform which in turn yields change in their apparent behavior and properties. Materials with such switchable properties have applications in the development of soft robots, but could also be used to tune their acoustic properties, for example, for sound filtering and noise mitigation.
To develop such (meta-)materials, it is advantageous to be able to simulate them, which means we determine the mechanical properties of a material with a certain microstructure, by simulating one representative volume element (RVE) of the material (i.e., a periodically repeating unit). Due to the very large deformations and complex non-linear behavior that happen, these simulations can be very costly. This is why we would like to develop a surrogate model using graph neural networks.
The input to such a simulation is the global deformation F (affine), whereas the output is the full deformation, as well as global quantities (strain energy density [a scalar], stress tensor [a 2nd order geometric tensor], and stiffness [a 4th order geometric tensor]).
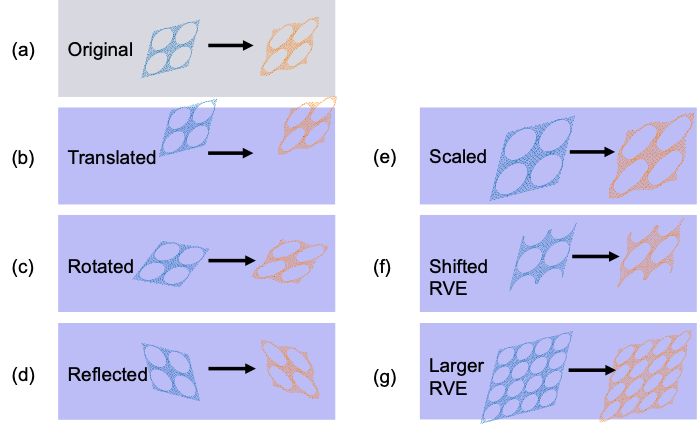
For these simulations, certain equivariances apply, reflecting the underlying governing equations. This means that when the input is transformed a certain way, the output transforms the same way. The relevant equivariances are translation, rotation, reflection equivariance (together these are called E(n)-equivariance), as well as scale equivariance and periodicity.
Currently, we are using the method described by Satorras et al [1] to incorporate the E(n)-equivariance, but there are more options.
References
· [1] Satorras, V. G., Hoogeboom, E., & Welling, M. (2021). E(n) Equivariant Graph Neural Networks. http://arxiv.org/abs/2102.09844
· [2] Gasteiger, J., Giri, S., Margraf, J. T., & Günnemann, S. (2020). Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules. https://arxiv.org/abs/2011.14115v3
· [3] Schütt, K. T., Unke, O. T., Gastegger, M., Schütt, S., Unke, O. T., & Gastegger, M. (2021). Equivariant Message Passing for the Prediction of Tensorial Properties and Molecular Spectra. Proceedings of Machine Learning Research, 139, 9377–9388. https://proceedings.mlr.press/v139/schutt21a.html
· [4] Thomas, N., Smidt, T., Kearnes, S., Yang, L., Li, L., Kohlhoff, K., & Riley, P. (2018). Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. http://arxiv.org/abs/1802.08219
· [5] Batatia, I., Kovács, D. P., Simm, G. N. C., Ortner, C., & Csányi, G. (2022). MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields. http://arxiv.org/abs/2206.07697
· [6] Hanocka, R., Hertz, A., Fish, N., Giryes, R., Fleishman, S., & Cohen-Or, D. (2019). MeshCNN: A network with an edge. ACM Transactions on Graphics, 38(4), 12. https://doi.org/10.1145/3306346.3322959
Details
- Supervisor
-
 Vlado Menkovski
Vlado Menkovski
- Secondary supervisor
-
OHOndrej Rokos, Fleur Hendriks
- Interested?
- Get in contact