Project: Understanding deep learning: efficient retraining of networks
Description
Recent work has shown that neural networks, such as fully connected networks and CNNs, learn to distinguish between classes from broader to finer distinctions between those classes [1,2] (see Fig. 1).
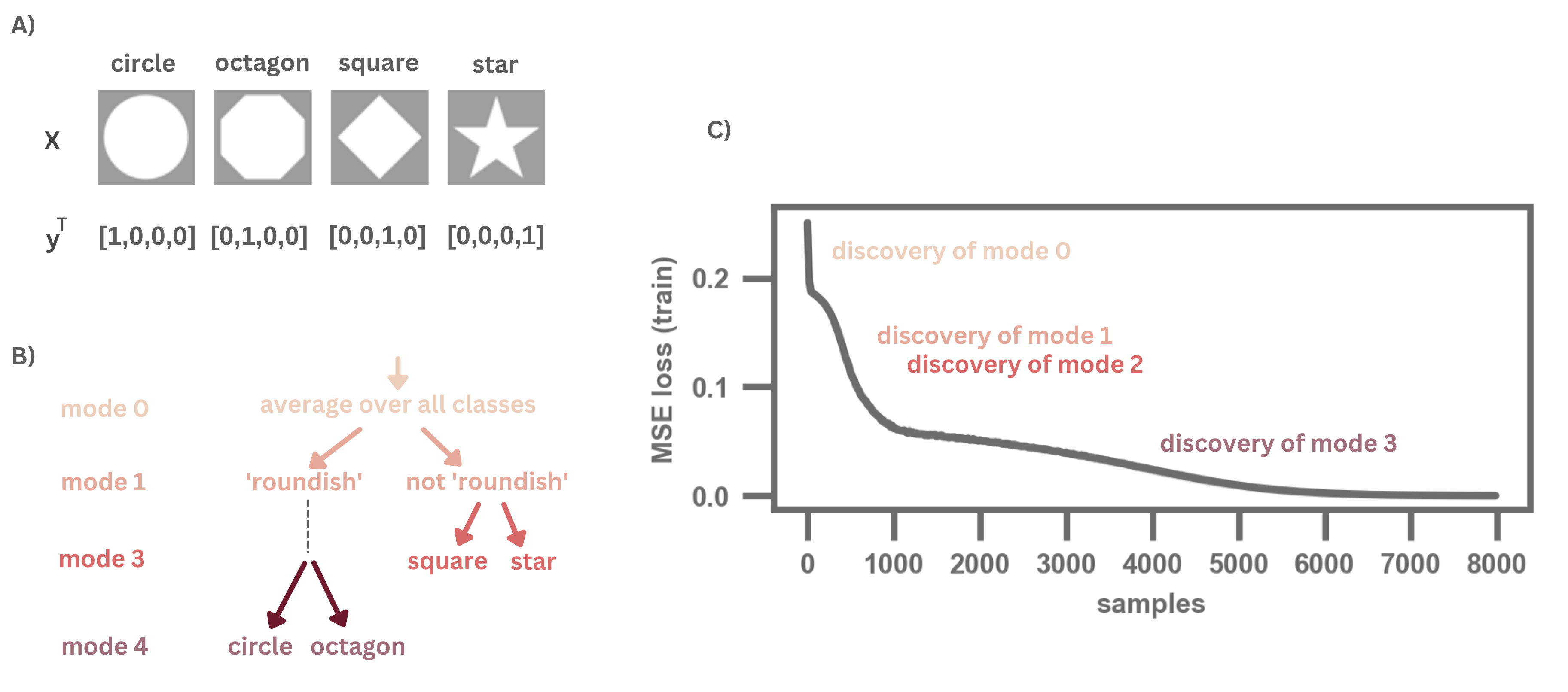
Figure 1: Illustration of the evolution of learning from broader to finer distinctions between classes. A) Example dataset consisting of figures of different geometric figures. B) From this dataset, we can use a singular data composition to obtain a notion of the inherent dataset structure. Here this structure (or the different modes of the decomposition) is a hierarchical structure representing broader to finer distinctions between classes. C) When we train a simple network on this dataset with an MSE loss, we see that the drops in the loss correspond to the network discovering the broader to finer distinctions. See reference [2] for more details.
These broader to finer distinctions are based on a singular value decomposition (SVD) of the dataset and can be computed beforehand; the order of learning is then given by the associated singular values. The theory behind this phenomenon has been developed for shallow, linear neural networks, but the phenomenon is exhibited by deep, non-linear networks as well. In short, we thus understand some important aspects of what and when neural networks learn.
In this project, we will try to make use of this information for settings where the networks need to be retrained, e.g., for concept drift or transfer learning. When we wish to retrain the network, could we then make use of our knowledge of when and how the network learned to restore it to an earlier state that would lead to an efficient retraining?
In this project, you thus would try to answer the following questions:
how well can we identify concept drift (or the difficulty of new tasks) using the given mathematical tools
how can we identify a useful previous state to retrain from, and does this lead to more efficient retraining with respect to other approaches?
what are the drawbacks and limitations of this approach?
Skills needed: basic linear algebra and basic understanding of differential equations, understanding of deep learning architectures, good programming skills.
[1] Saxe, A. M., McClelland, J. L., & Ganguli, S. (2019). A mathematical theory of semantic development in deep neural networks. Proceedings of the National Academy of Sciences, 116(23), 11537-11546.
[2] Pinson, H., Lenaerts, J. & Ginis, V.. (2023). Linear CNNs Discover the Statistical Structure of the Dataset Using Only the Most Dominant Frequencies. In International Conference on Machine Learning (pp.27876-27906). PMLR.
Details
- Supervisor
-
 Hannah Pinson
Hannah Pinson